UQ of Tracer Transport in the Cochlear Aqueduct

Tracers injected into the cerebrospinal fluid that surrounds the brain reach the inner ear via the so-called cochlear aqueduct (CA). The recent discovery of a membrane in the aqueduct raises questions about the restrictions of transport between the compartments and implications on the delivery of therapeutics to the inner ear to rescue hearing. A CT study was conducted to quantify the diffusive and advective modes of transport through the aqueduct in mice.

In a joint work with Peter A. R. Bork and Barbara Koch Mathiesen from the Center for Translational Neuromedicine at Copenhagen University, we estimate the transport model parameter, allowing the diffusivity to vary in space with potential membranes. The computations utilize the PDE-based inverse problem facilities in the CUQIpy software.

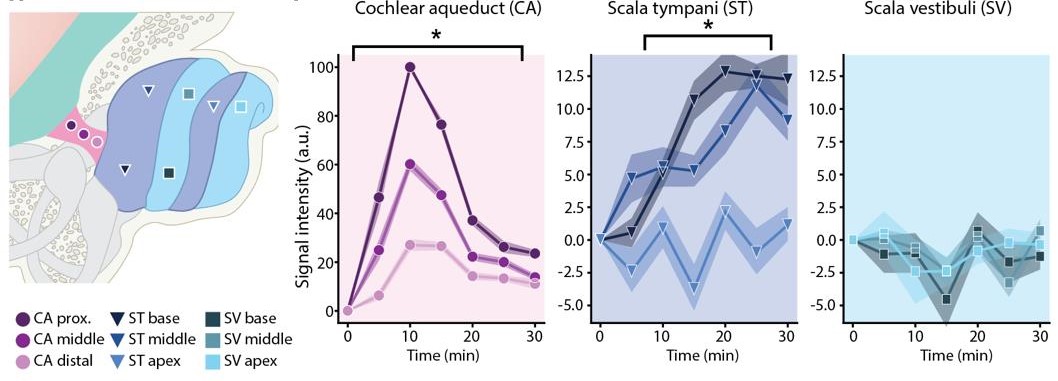
The above figure from Mathiesen et al. (2023) shows tracer concentration measurements at various locations in the CA and the cochlea. The forward model has the form y_obs = A(x) + noise, where x represents the unknown spatially varying diffusivity and advection speed, the data y_obs is the concentrations at given times and locations in the CA, and A represents a PDE-based forward model in the form of a time-dependent diffusion equation:

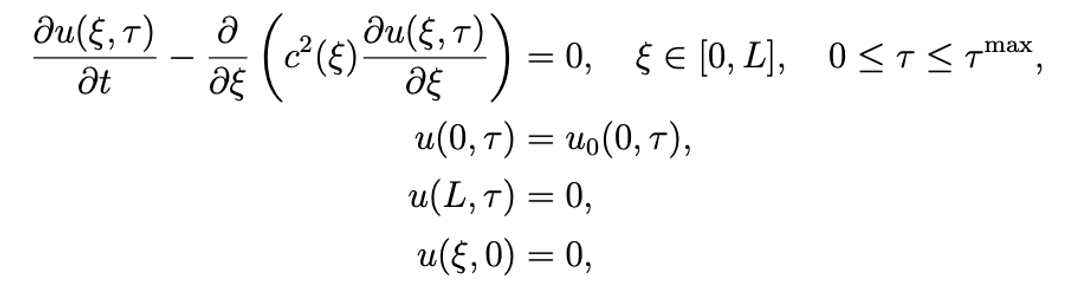
The PDE is discretized using first-order finite differences in space and backward Euler in time.

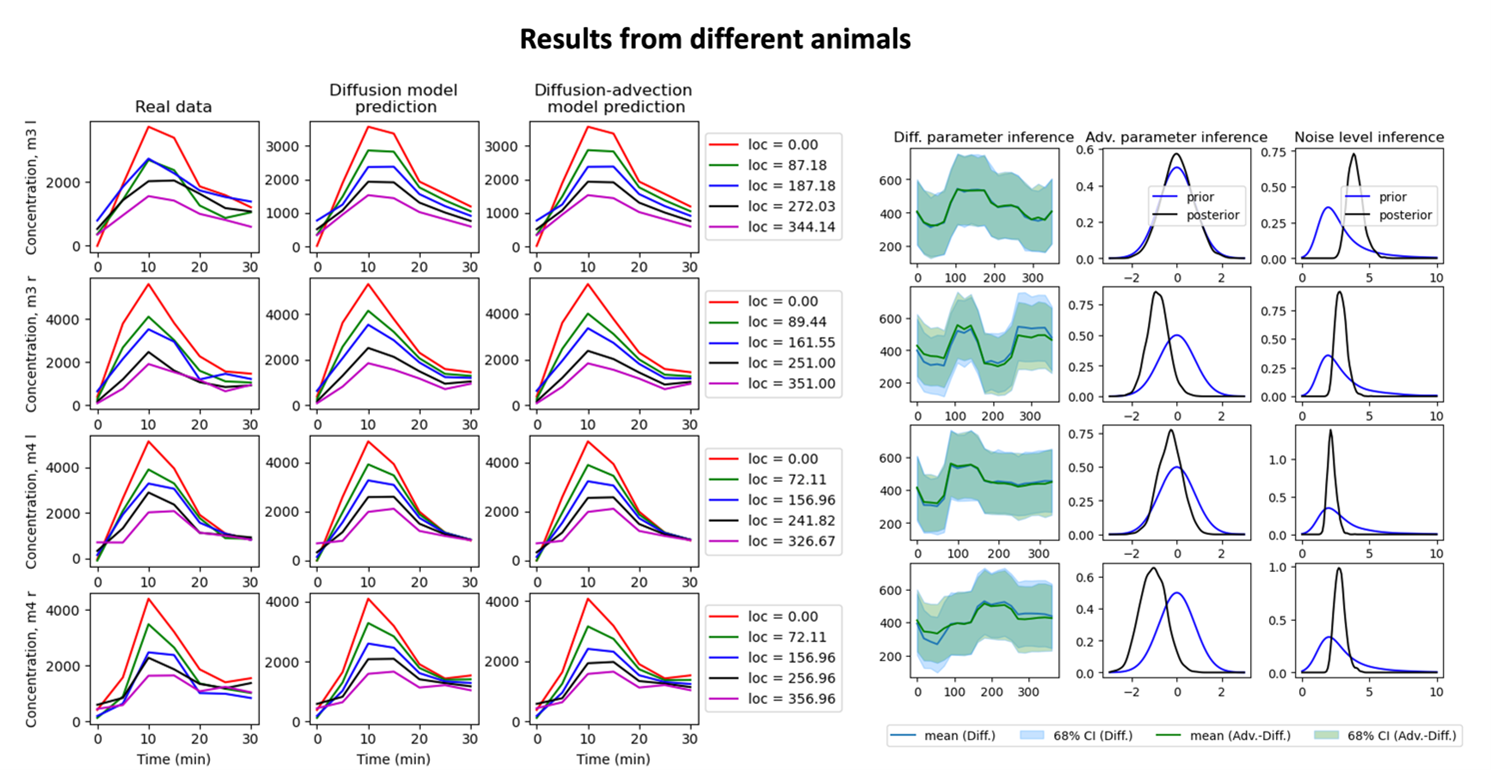
The figure below shows computational results using data from different mice. These preliminary results illustrate the identification of a spatially varying diffusivity in the CA. Moreover, small advection of various degrees is detected in some cases.

Below are elements of the CUQIpy code for the simulations.

The Bayesian Approach to Inverse Robin Problems in Ice Flow

Ice-sheet models are important components of long-term sea level predictions. A crucial model parameter is the basal drag coefficient, which is a spatially varying parameter that models the slipperiness of the lubricating sediment beneath the ice.

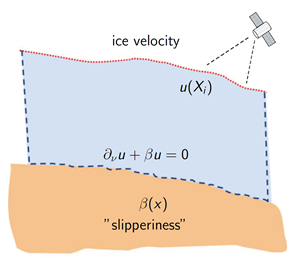
The ice flow can be modeled by a Stokes system of partial differential equations, where the basal drag coefficient β enters in a Robin boundary condition on the bottom part of the ice boundary. On the surface of the ice, we make N observations Y_i of the ice velocities at locations X_i picked uniformly at random:
     Y_i = u(X_i) + ε_i ,   i = 1,...,N .
Here, u is the ice velocity that depends on β and ε_i is Gaussian noise. Estimation of β is a nonlinear and severely ill-posed inverse problem known as an inverse Robin problem.

From a mathematical point of view little is known about the reliability of the Bayesian approach for such nonlinear inverse problems. But if we use Gaussian priors with a favorable covariance structure then more can be said. As an example, consider two Gaussian priors suited for estimating β on the interval [0,1]: the Matérn prior and the squared-exponential Gaussian prior, samples of which are shown below.

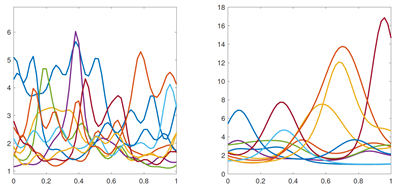
For these two choices of priors, we can guarantee that the Bayesian approach is reliable when applied to a simplified inverse Robin problem. If the ground truth β is Sobolev regular of some index, then the posterior mean from a suitable Matérn prior converges to β (in prob.) at a logarithmic rate as N → ∞. Similarly, if β is analytic (very smooth) then we have convergence for the squared-exponential prior at rate N^−σ as N → ∞.

The figure below shows the ground truth, the conditional mean, and samples from the posterior using the Matérn prior (top) and the squared-exponential prior (bottom). We see that there is less uncertainty for the latter prior in this example.

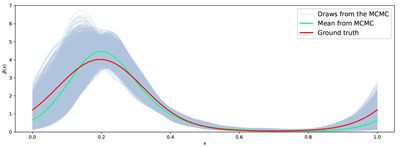
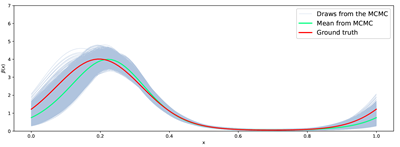
This work was carried out by PhD student Aksel Kaastrup Rasmussen and it is documented in the paper with Seizilles, Girolami & Kazlauskaite (2023). Software is available as a CUQIpy notebook.

Boundary Detection in X-Ray CT Applications

In 2D CT, every X-ray going through the object is characterized by its slope θ with the horizontal axis. In practice, a full-angle geometry where θ covers the entire interval [0,π) is not always possible. This could be due to obstacles in the CT measurement setup or to avoid unhealthy levels of radiation exposure. In such cases, a limited-angle geometry is needed, i.e., θ belongs to the reduced interval [0,θ_max) with θ_max ≪ π. In such a setup, the quality of reconstructed image is compromised when conventional reconstruction methods are applied.

In many X-ray CT applications, the boundaries of objects - as well as their roughness - contain valuable information, e.g., to differentiate between benign and malignant tumors. Confidence in estimating such features helps with an accurate diagnosis and designing an effective treatment plan. A common approach in detecting boundaries is via an image segmentation post-processing step, but the quality of the estimated boundaries is compromised in the limited-angel case.

We provide a novel goal-oriented, Bayesian framework for the limited-angel CT problem, in which we reconstruct the boundaries directly from the data without the need for reconstructing the image. Moreover, we quantify the uncertainty of the boundaries and their roughness. This approach avoids error propagation and reduces the dimensionality of the problem from finding a 2D image to a 1D boundary of a region.

Our key ingredient is a hierarchical Bayesian approach to estimating the roughness of a scalar function, based on a Whittle-Matérn covariance prior and the level of fractional differentiability. We also developed an efficient FFT-based computational method for implementing this. Numerical results indicate that this framework is a promising and effective tool for solving a broad range of inverse problems where the regularity of functions carries critical information.

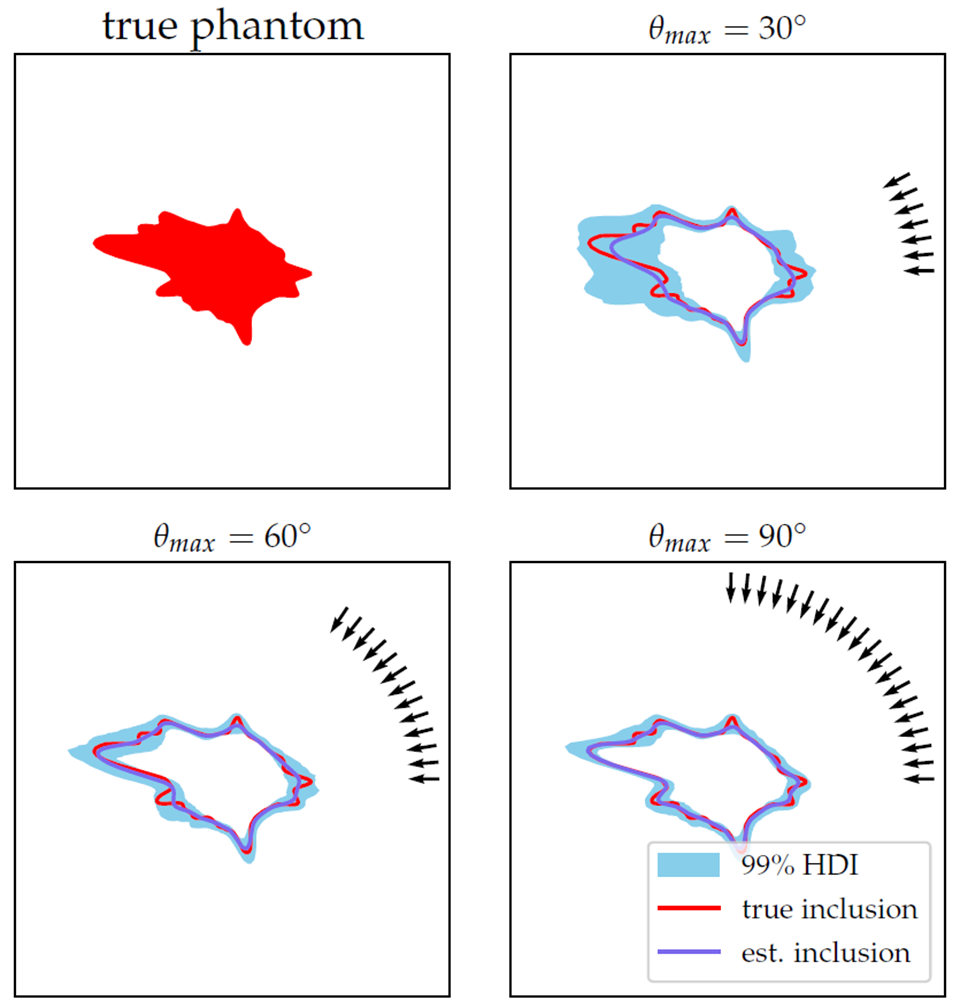
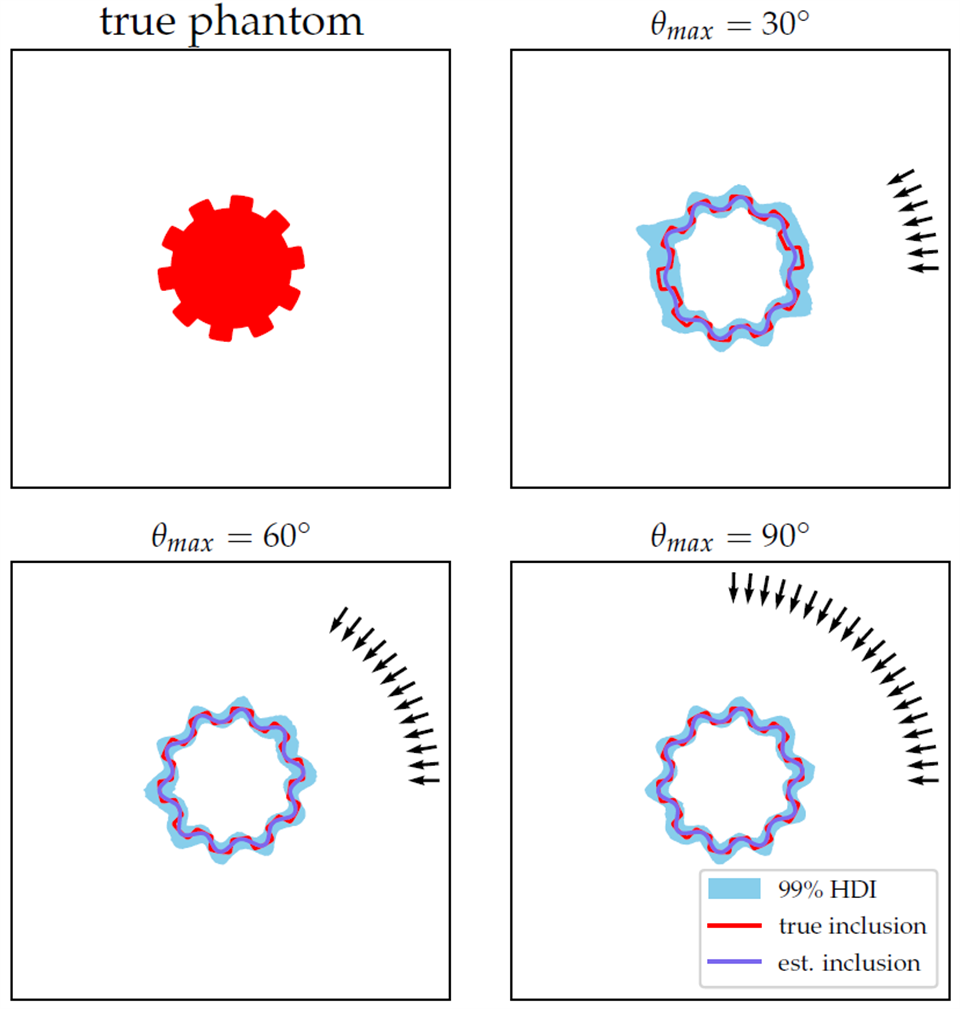
The above plots show the performance of our method in estimating the boundaries of an object in the limited-angle setup with different θ_max. The arrows indicate the angles of the X-rays and thus region of the limited-angle interval [0, θ_max). The estimated boundaries are shown in dark blue color, and the light blue region indicates the uncertainty in this estimation. The smaller the θ_max the larger the uncertainty region - which is consistent with the results from microlocal analysis.

For more details, see the SIAM/ASA paper by Afkham, Dong & Hansen (2023) and the paper in J Math Imaging Vis by Afkham, Riis, Dong & Hansen (2024).

Defect Detection in X-Ray CT of Subsea Pipes

X-ray computed tomography (CT) is used to monitor the condition of subsea oil or gas pipes in operation, in order to detect defects that might cause leaks. In this example, we use data obtained in the test facilities at FORCE Technology. Computations are done with our CUQIpy software which draws upon the Core Imaging Library (CIL) for the CT models.

We formulate a Bayesian inverse problem with built-in defect detection. The goal is to detect defects and quantify their uncertainties. We express the CT problem as y = A (x+d) + e, where y is the measured X-ray absorption, e is data noise, and A is the linear forward model representing the physics and geometry of the measurements. We use a novel representation x + d of the unknown image to be reconstructed, expressed as a sum of two images; x contains the pipe structure and d contains potential defects.

In the Bayesian setting we formulate the joint posterior distribution p(x,d | y) ∝ p(y | x,d) p(x) p(d), where p(x,d | y) is the joint posterior distribution representing the solution to the CT problem, p(y | x,d) is the likelihood that represents the data misfit, while p(x) and p(d) are prior distributions representing any knowledge we have about the unknown images.

We impose priors that promote the structures we are looking for. For the pipe structure x, we use the structural Gaussian prior proposed by Christensen, Riis, Uribe & Jørgensen (2023). The above figure shows a sample from this prior which promotes the known layered pipe structure. We expect small and few defects, and therefore we impose a prior that promotes both sparsity and correlation (a gamma Markov random field) in the defect image d as described in the paper by Christensen, Riis, Pereyra & Jørgensen (2023). We explore the conditional posterior distributions p(x | y,d) and p(d | y,x) using Gibbs sampling.

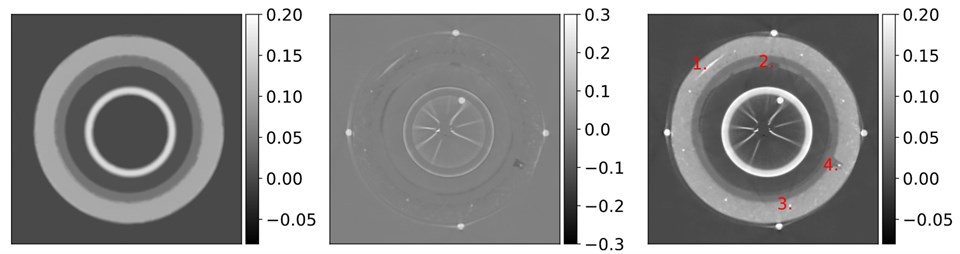
The figure above shows the means of the x-samples (left), the d-samples (middle), and their sum with annotation (right). These results indicate that our methodology has successfully separated the defects from the overall pipe structure. In the figure below we zoom-in on the defect reconstruction d for the annotated defects indicated in the figure above, for further investigation of these defects. The figure shows the mean of the posterior samples, as well as related UQ in the form of the standard deviation of the samples. Engineers can use these results to identify critical defects in the subsea pipes.

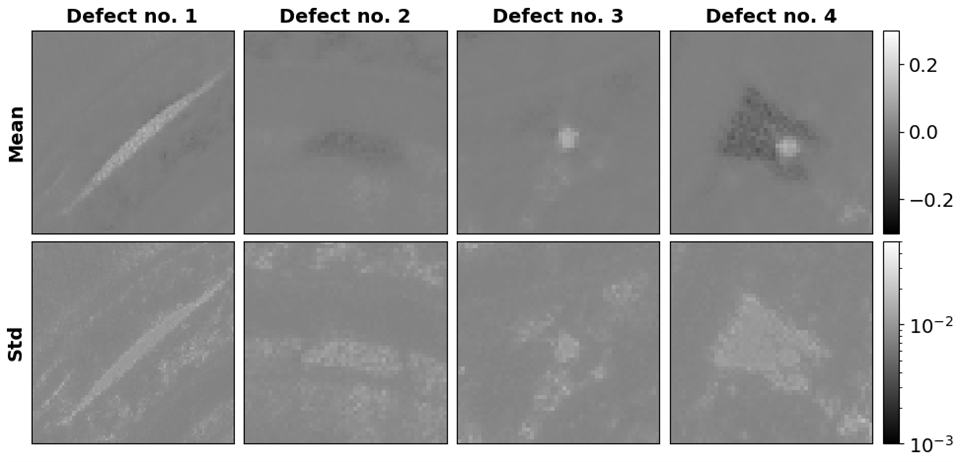
This is joint work with Prof. Marcelo Pereyra from Heriot-Watt University. The example was created by PhD student Silja L. Christensen.

Bayesian Inference with Constraints

In many applications, the reconstruction must satisfy certain constraints, e.g., material densities are positive, image intensities are between 0 and 1, or the energy of a signal is bounded. Adding such prior information to a Bayesian model improves the meaningfulness of the resulting posterior distribution.

A common method to model constraints in a prior distribution is truncation: choose an unconstrained prior distribution and remove all probability outside of the constraint set. Another method is to reparametrize the signal, e.g., if the signal x is assumed to be positive, then it can be written as x = exp(z) and one can use an unconstrained prior distribution for z. These methods focus on the interior of the constraint set, but sometimes the signals of interest lie on the boundary of the constraint set.

As an alternative, one can first sample from an unconstrained posterior distribution and then apply a suitable projection onto a convex constraint set C. The resulting implicit posterior will consist of the original density in the interior of the constraint set, and a “lower-dimensional” distribution on the boundary, see the illustration below.

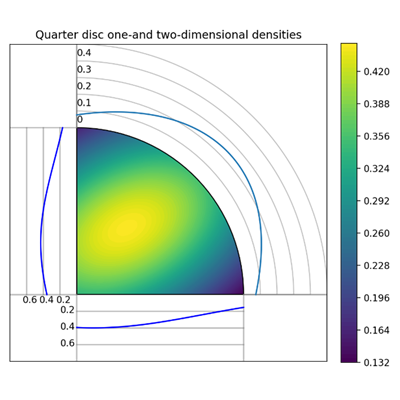
If the forward model is linear and both the likelihood and prior are Gaussian distributions, then the unconstrained sampling and projection can be done in a single step by repeatedly solving randomized constrained linear least square problems of the form

min_x∈C || A x - b_s ||₂² + α || x - c_s ||₂² ,

where b_s and c_s are samples from suitable distributions. The solutions to these optimization problems will be samples of a projected posterior.

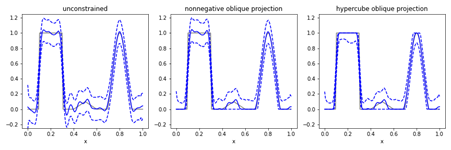
Consider the problem of deblurring a noisy 1D signal with prior knowledge that the signal lies in the interval [0,1]. The figure above shows the pointwise median and 99% credible interval for such a problem using no constraints (left), only the nonnegativity constraint (middle), and the box constraint (right). The projection framework significantly improves the quality of the median near the boundary.

This feature is now available in our CUQIpy software.

See the SIAM-ASA paper Everink, Dong & Andersen (2023).

The Horseshoe Prior for Edge-Preserving Reconstruction

If we want to reconstruct an image with sharp edges, we can use a Cauchy or Laplace distribution of the difference between neighbor pixels as the prior (this is related to total variation regularization). Unfortunately, these priors are computationally demanding. As a computationally attractive alternative, we can use a so-called horseshoe prior that resembles the Cauchy and Laplace priors - see the figure below where the horseshoe prior's density is guaranteed to lie in the shaded band.

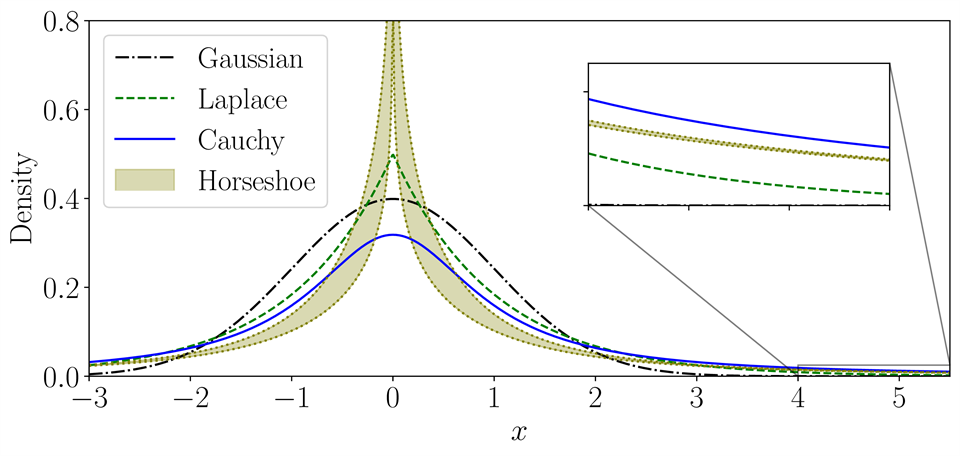
The main advantage of the horseshoe prior is that it imposes a conditionally Gaussian distribution on the differences, which allows more efficient computations because Gaussians can be handled with efficient least-squares methods. The difficulty is that the horseshoe prior has hyperpriors with heavy tails, and to alleviate this issue we propose an extended horseshoe prior that uses a scale-mixture representation of the heavy-tailed hyperpriors.

For the posterior, we exploit the extended horseshoe prior to compute conditional distributions for the associated parameters that can be sampled in closed form due to conjugacy. This allows the application of a Gibbs sampler.

Here we illustrate our method with a 1D deconvolution problem for two different noise levels, and we compare with posterior statistics obtained with a Laplace-difference prior proposed by Uribe, Bardsley, Dong, Hansen & Riis (2022).  Compared to the Laplace-difference prior, we see that the horseshoe prior gives a sharper posterior (dotted lines) and a lower posterior uncertainty (the shaded area shows the 95% credibility interval). The solid line shows the ground truth.

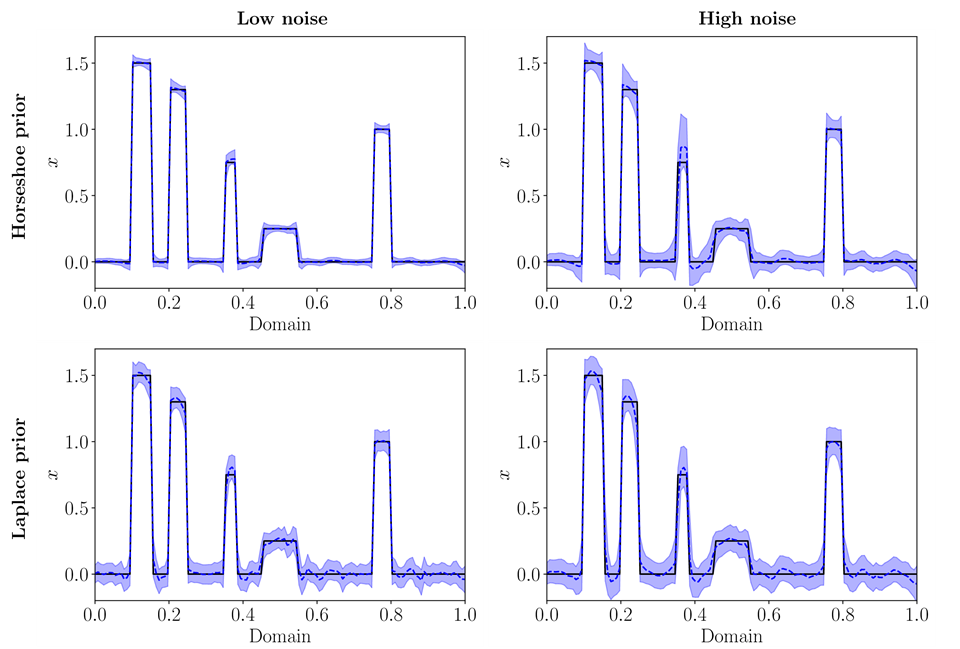
The horseshoe prior originated in the statistical community, and here we introduce it in the setting of Bayesian inverse problem - see the paper by Uribe, Dong & Hansen (2023).

Dimension Reduction for High-Dimensional Problems

A persistent challenge is efficient sampling of high-dimensional posteriors. Using a bigger/faster computer might help, but the breakthrough comes from the use of clever mathematical models and methods.

Rafael Flock developed a novel method using certified coordinate selection that focuses on those solution components that contribute the most to the update from the prior to the posterior. After identification of these components, a dimension-reduced posterior approximation is constructed by replacing the likelihood function by a ridge approximation that only lives in the much lower dimensional space of the selected coordinates – thus saving substantial computational work.

The method is illustrated with an example from super-resolution microscopy where the goal is to compute accurate positions of fluorescence photoactivated molecules, via application of stochastic optical reconstruction microscopy (STORM). The image below shows the data (photon counts) in the form of a blurred image of the molecules.

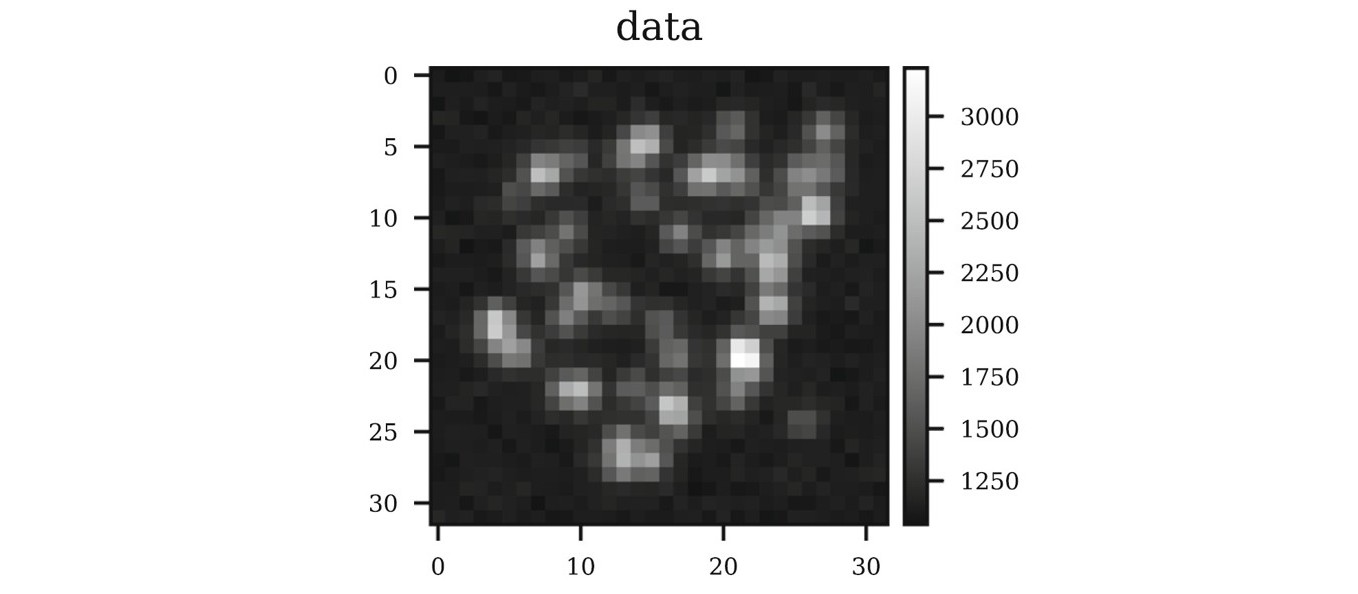
The next two images show the true molecule positions (white dots) superimposed on 1000 coordinates (red dots) that were selected using the certified coordinate selection method and the 99% credible intervals (CI) obtained via MCMC simulation on the dimension-reduced posterior in log10-scale for better visibility.

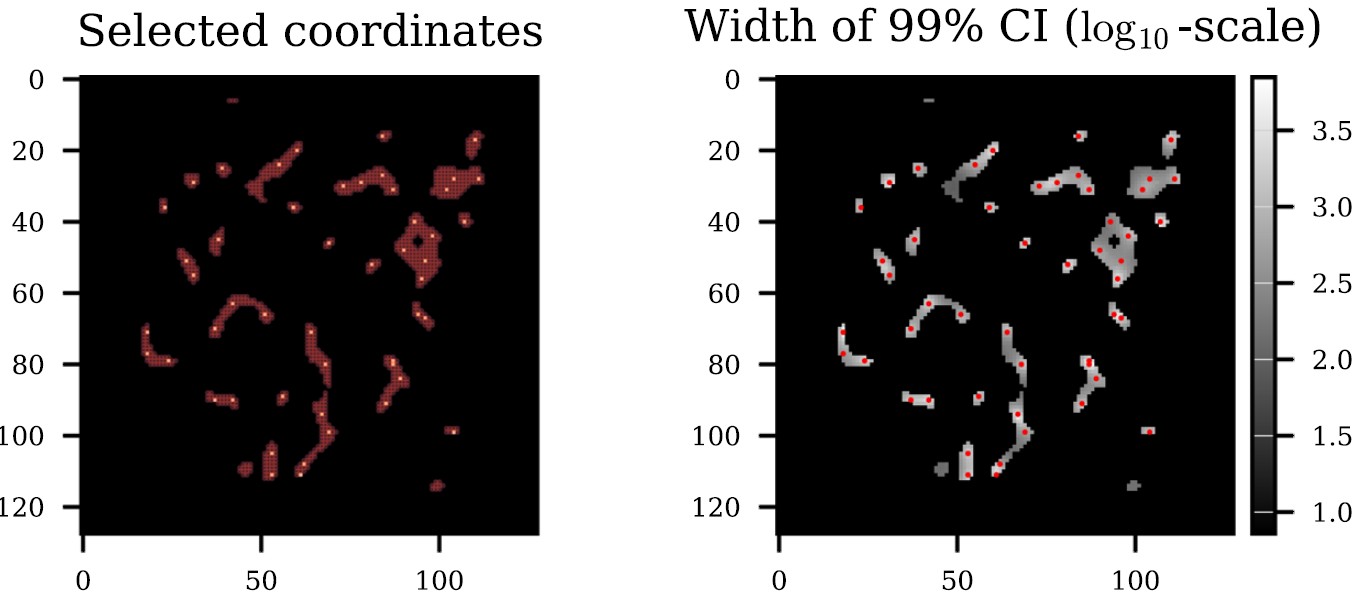
This work is described in a paper by Flock, Dong, Uribe & Zahm.

Bayesian Inversion with Collision Physics

Nuclear fusion can potentially deliver steady and safe power without causing global warming.

A tokamak reactor (such as DTU's NORTH seen above) uses a magnetic field to confine plasma where energy is produced through fusion. To monitor the plasma, we compute the velocity distribution of the plasma ions via solving a tomography problem using measurements of Doppler shift of photons generated in the plasma.

To solve the corresponding inverse problem, we impose a prior that expresses to actual physics of the ions being slowed down due to collisions inside the plasma. This is done by expressing the solution – i.e., the velocity distribution – in terms of basis functions that represent the collision physics.

In the Bayesian setting of the inverse problem we show (see these slides) that the solution’s covariance matrix is always given by C ∝ Ψ Ψ^T, where Ψ is matrix whose columns are the basis vectors that represent the collision physics. This allows us to determine the localized correlations in the velocities. In an energy-pitch (E,p) system we see that for a lower energy the correlation in pitch increases, see the figure below.

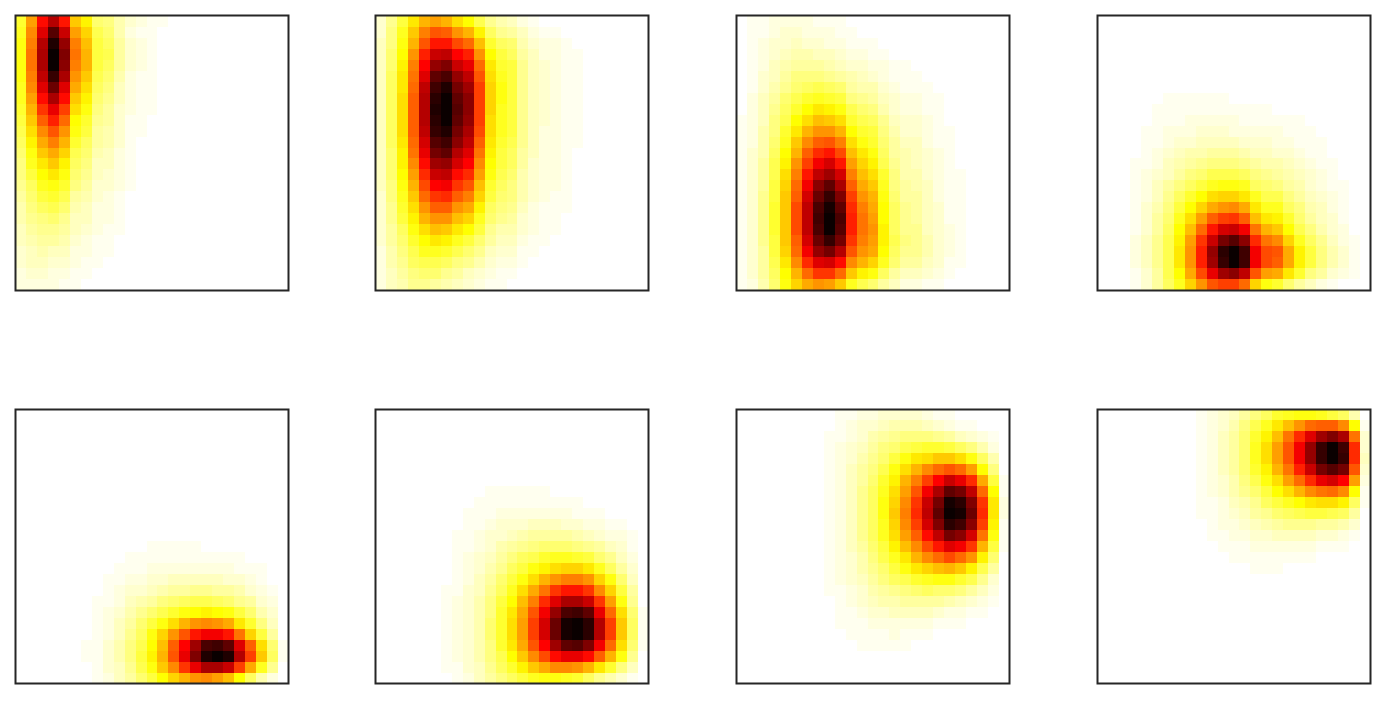
This collaboration involves, among others, Y. Dong and P. C. Hansen from CUQI, Prof. M. Salewski and postdoc Mads Rud Larsen from DTU Physics, and postdoc B. S. Schmidt from UC Irvine.

Follow this LINK to see pictures from our team building event in the spring of 2023.

Specialist in convex optimization and numerical optimization algorithms.

Specialist in noise modeling and computational methods for image processing.

Link to portrait.

Specialist in numerical analysis, iterative solvers, and computational methods for inverse problems.

Link to portrait.

Specialist in methods and software for image reconstruction and their application in X-ray CT.

Specialist in functional analysis and physical modeling with uncertainty quantification.

Specialist in coupled-physics modeling, PDE-constrained optimization, functional analysis and electrical impedance tomography.

Link to portrait.

Executive advisor and project coordinator.

Project secretary.

Project: computational UQ for PDE problems.

Project: optimization-based sampling in Bayesian inverse problems.

Project: discretization methods for tomography.

Project: large-scale computational UQ for inverse problems.

Former Postdocs

Project: goal-oriented UQ.

Now with Univ. of Oulu.

Project: machine learning and UQ for inverse problems.

Now works with explainability in AI at EDF R&D in Paris.

Project: efficient and flexible computational methods.

Now works with software development at Copenhagen Imaging; homepage.

Project: non-Gaussian priors.

Now with Danfoss Leanheat, Finland; homepage.

Project: Bayesian inference for inverse problems with sampling conditioned on functionals.

Project: inverse problems with Besov prior.

Former PhD Students

Sept. 1, 2019 to June 30, 2023 (incl. parental leave).

Project: prior modeling in computational UQ for inverse problems.

Thesis: Bayesian modeling and uncertainty quantification with applications in computed tomography and hemodialysis.

Katrine is now a Senior Modelling Scientist with Novo Nordisk Research & Development.

August 1, 2020 to May 27, 2024 (incl. parental leave).

Project: UQ for tomographic reconstruction.

Thesis: Prior modeling and uncertainty quantification in X-ray computed tomography with application to defect detection in subsea pipes.

Silja was a research assistant in CUQI June-October 2024. She is now a geophysicist with COWI, Denmark.

Oct. 1, 2021 to Sept. 30, 2024.

Project: Computational Uncertainty Quantification for Inverse Problems with Implicit Priors.

Jasper is now a postdoc in CUQI.

Oct. 1, 2021 to Sept. 30, 2024.

Project: Dimensionality challenges in UQ for inverse problems.

Rafael was a postdoc in CUQI October-December 2024. He is now with WTM Engineers in Hamburg.

Sept. 1, 2020 to Aug. 31, 2023.

Project: computational UQ of hybrid inverse problems.

Thesis: On deterministic and statistical consistency for nonlinear inverse problems.

Aksel was a research assistant in CUQI November-December 2023. He is now a Principal Biostatistician with H. Lundbeck A/S.

Nov. 1, 2021 to Jan. 31, 2024.

Project: model error reduction in inverse problems.

Puyuan stopped before getting his degree.

Feb. 1, 2021 to Jan.31, 2024.

Project: UQ for source localization and passive imaging in random media.

Thesis: Uncertainty quantification for source localization and passive imaging in random media.

Kristoffer is now postdoc in the Villum Experiment project neXt-Ray: a super-resolution light engine.
.

Assistant Professor Babak M. Afkham, assistant professor, Mathematical Sciences, University of Oulu - specialist in goal-oriented UQ and PDE-based inverse problems.

Professor Johnathan M. Bardsley, Department of Mathematical Sciences, University of Montana - specialist in computational methods for inverse problems and uncertainty quantification.

Associate Professor Julianne Chung, Department of Mathematics, Emory University - specialist in in computational methods for inverse problems and uncertainty quantification in imaging applications.

Associate Professor Matthias Chung, Department of Mathematics, Emory University - specialist in computational inverse problems, data analytics & learning, uncertainty quantification, and numerical optimization.

Professor Bangti Jin, Department of Mathematics, Chinese University of Hong Kong - specialist in theory and algorithms for inverse and ill-posed problems.

DTU Compute, Section for Mathematics - specialist in wavelets, frames, and signal analysis.

Professor Marcelo Pereyra, Maxwell Institute for Mathematical Science and School of Mathematical and Computer Sciences, Heriot-Watt University - specialist in statistical, analytical and machine-learning paradigms.

Software Development Manager Nicolai A. B. Riis, Copenhagen Imaging - specialist in scientific software.

Professor Tanja Tarvainen, Department of Applied Physics, University of Eastern Finland - specialist in computational methods for inverse problems and uncertainty quantification in imaging applications

Research Professor Faouzi Triki, Laboratoire Jean Kuntzman, Grenoble-Alpes University - specialist in inverse problems and mathematical modeling in optics.

Data scientist Felipe Uribe, Danfoss Leanheat, Finland - specialist in applied probability & statistics, and large-scale sampling methods.

Research Scientist Olivier Zahm, INRIA-Grenoble - specialist in model order reduction for uncertainty quantification.